In previous articles I have discussed how global climate (and other systems) may evolve rapidly from one condition to another.
In describing the transition from one state to another I have been using a statistical computational method akin to Markov chains to create a descriptive finite state machine (which I have previously referred to as epsilon machines).
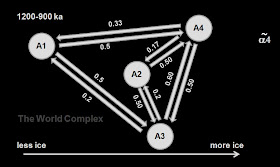
Finite state machines normally consider that there is some sort of impulse or input which drives the transition, and the exact value of the input controls defines which particular successor state follows from a predictive state. For systems like global climate, we do not know what the external forcing, so we cannot create a matrix showing the dependence of state transitions on the forcing. Instead I have calculated the probability of each successor state following a predictive state purely from the observed sequence of states.
For instance, in the chart above, from state A3, the system shifts to A1 20% of the time, to A2 20% of the time, and to A4 60% of the time. Perhaps there were five observed transitions from state A3. The probabilities have been computed on the basis of a single predictive state. There is an argument that the evolution of the system is a function of the entire past history, suggesting we should really consider more than one sequential state for prediction. I have not done this because there are not enough transitions to determine such a matrix.
Conventional thinking is that a state change is driven by some external forcing. I have generally assumed that this is not the case, but that the observed discontinuities arise from a smooth evolution of one or more underlying parameters. Such discontinuities can be referred to as catastrophes.
Today's discussion is a reflection on catastrophe-- in particular, how a system governed by gradual, continuous changes in key parameters can bring about the appearance of sudden, discontinuous change.
One way to visualize how slow, continuous change can bring about a discontinuous response is through the use of a quartic function. In this case, we will use y = x^4 - 1.5 x^2 + a (x - 0.5) + 1. A family of such curves is presented below, for values of a ranging from -1.2 to 1.6.
The general form of the curve is two wells separated by one high point. Place a yellow marble in the right well (with a = -1.2), and consider its position as a gradually varies from -1.2 to 1.6.
At some point, (it is difficult to tell just when, visually), the well at the right will disappear, and the marble will roll down into the well at the left. We can calculate for which value of a this occurs. At each of the minimum and maximum points, the first derivative of the function is zero. The derivative of the expression above is:
y' = 4 x^3 - 3 x + a
We can see by inspection that when a = 1, two solutions degrade into one (at x = 0.5). This point is an inflection point, neither a maximum nor a minimum.
The position of the ball suddenly changes from 0.7 to -1 at a = 1.
The well on the left disappears at a = -1, so if we ran the experiment in reverse, we would see the jump at a = -1. This phenomenon is known as hysteresis. We would describe the change above as irreversible, as restoring the condition of the system to just before the discontinuity does not reverse the change.
If we studied some system with the above behaviour, conventional thinking would have some large input right at around a = 1. In reality, as we see, the jump happens when the system passes the tipping point.
Does climate behave like the mathematical function described above? There is growing agreement that it does, however the probability of such an event in our near future cannot realistically be assessed (Livina's comments to the contrary on page 8 of the linked pdf).
In describing the transition from one state to another I have been using a statistical computational method akin to Markov chains to create a descriptive finite state machine (which I have previously referred to as epsilon machines).
Finite state machines normally consider that there is some sort of impulse or input which drives the transition, and the exact value of the input controls defines which particular successor state follows from a predictive state. For systems like global climate, we do not know what the external forcing, so we cannot create a matrix showing the dependence of state transitions on the forcing. Instead I have calculated the probability of each successor state following a predictive state purely from the observed sequence of states.
For instance, in the chart above, from state A3, the system shifts to A1 20% of the time, to A2 20% of the time, and to A4 60% of the time. Perhaps there were five observed transitions from state A3. The probabilities have been computed on the basis of a single predictive state. There is an argument that the evolution of the system is a function of the entire past history, suggesting we should really consider more than one sequential state for prediction. I have not done this because there are not enough transitions to determine such a matrix.
Conventional thinking is that a state change is driven by some external forcing. I have generally assumed that this is not the case, but that the observed discontinuities arise from a smooth evolution of one or more underlying parameters. Such discontinuities can be referred to as catastrophes.
Today's discussion is a reflection on catastrophe-- in particular, how a system governed by gradual, continuous changes in key parameters can bring about the appearance of sudden, discontinuous change.
One way to visualize how slow, continuous change can bring about a discontinuous response is through the use of a quartic function. In this case, we will use y = x^4 - 1.5 x^2 + a (x - 0.5) + 1. A family of such curves is presented below, for values of a ranging from -1.2 to 1.6.
The general form of the curve is two wells separated by one high point. Place a yellow marble in the right well (with a = -1.2), and consider its position as a gradually varies from -1.2 to 1.6.
At some point, (it is difficult to tell just when, visually), the well at the right will disappear, and the marble will roll down into the well at the left. We can calculate for which value of a this occurs. At each of the minimum and maximum points, the first derivative of the function is zero. The derivative of the expression above is:
y' = 4 x^3 - 3 x + a
We can see by inspection that when a = 1, two solutions degrade into one (at x = 0.5). This point is an inflection point, neither a maximum nor a minimum.
The position of the ball suddenly changes from 0.7 to -1 at a = 1.
The well on the left disappears at a = -1, so if we ran the experiment in reverse, we would see the jump at a = -1. This phenomenon is known as hysteresis. We would describe the change above as irreversible, as restoring the condition of the system to just before the discontinuity does not reverse the change.
If we studied some system with the above behaviour, conventional thinking would have some large input right at around a = 1. In reality, as we see, the jump happens when the system passes the tipping point.
Does climate behave like the mathematical function described above? There is growing agreement that it does, however the probability of such an event in our near future cannot realistically be assessed (Livina's comments to the contrary on page 8 of the linked pdf).


I'd think hysteresis doesn't imply "IRreversibility" - just a large area of intertia on the graph that's positive in both directions. You can reverse the function, but you just have to take a different path.
ReplyDeleteEntropy goes both ways, that sort of thing.
Irreversible change (in these sorts of systems) usually is taken to mean harder to reverse than to change. If some dire change happens to earth's climate at, say, CO2 > 500 ppm, but it doesn't switch back unless CO2 < 250 ppm, it would be considered an irreversible change, even though it is reversible.
ReplyDelete