It's been awhile since we last checked in on Detour Gold Corp. (disclosure: long).
Over the past seven months, we have seen some nice price action, with a major rise in the early summer.
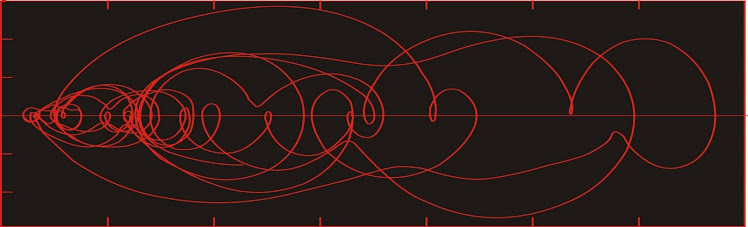
The two-d reconstructed phase portrait using the time-delay method with a lag of three days (as last time).
Over the past seven months, we have seen some nice price action, with a major rise in the early summer.
The two-d reconstructed phase portrait using the time-delay method with a lag of three days (as last time).
In our last installment on this stock the price was rising more or less monotonically. Now we see that what happened was a distinctive shift from one range (at lower left) to a higher price area, where the price has been bouncing around for awhile.
Looking at the two LSAs above, one represents a price range in the $21-25 range, and the second is $27-33. Should it fall out of this range, we would presume it could fall back into the other.
We can see a connection between the price chart and the reconstructed phase space portrait. It is clear that what we call confinement to a Lyapunov-stable area (and use as an indicator of at least temporary stability) . . .
. . . may be perceived by the chartists as "trading within a range".
(Those diagonal lines aren't intended to be there--they magically appeared during the conversion of the above chart from excel to corel to jpg).
If we look at the higher of the two Lyapunov-stable areas (LSA30), we see that different parts of it are occupied at different times.
Detail of LSA30 by month.
In particular, the regions of phase space centered at about $30 and at about $31.50 are visited at least three times, and several of those visits are characterized by small loops in the phase space portrait, suggesting quasi-stability. On the price chart above, those regions correspond with what chartists would call support and resistance.
The phase space portraits of complex systems are often characterized by areas of high probability density, which are sometimes (if they have the correct characteristics) called attractors, but may more commonly be referred to as Lyapunov-stable areas (LSA). An LSA is an area in phase space where the state of the system tends to remain assuming there are no dramatic changes in the dynamics of the system. We would normally interpret such an area as evidence for a metastable state in that region of phase space.
If the state space of the system normally occupies an area below the range of values represented within the LSA, then the upper and outer limit of values will appear (on a one-dimensional chart) to be resistance--and chartists frequently describe such phenomena as the price "bouncing" off resistance.
If the state space of the system is occupying the region above the LSA, the chartists will term the lower boundary of the LSA to be "support".
If support is broken, it means the system has left the LSA, and is moving towards another one, presumably at a lower price. The chartist will say that support has failed, and will look back along the chart for the next region of support, which will have been the lowest value of the next lower LSA. If the price has broken down through an all-time low, then there is no telling how low the price will go.
If resistance is broken, the price may move towards the next higher LSA if one is present. If so, the highest value within the LSA will be seen by the chartist as "the next area of resistance". If the price has broken to a new all time high, then we are probably all in the dark.