I will look at one approach for clarifying the phase space portraits we have constructed last time.
This approach is choosing a suitable embedding dimension, which is the number of dimensions of state space into which we will unfold our time series.
Embedding dimension
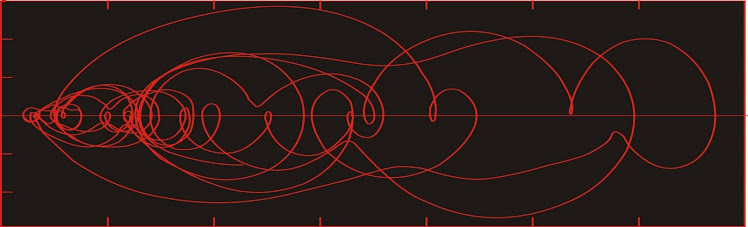
The curves in the reconstructed phase space should not intersect, if they are unfolded in the correct number of dimensions. The reason for this will become plain if we once again consider the reconstruction in terms of a function and all of its various time derivatives. Suppose that a system is completely described in a state space. These dimensions will be the scalar measurement, its first, second, and higher time derivatives (speed, acceleration, jerk, jounce or snap, etc.--in the scalar sense).
Each state is defined by a "position" in phase space, with coordinates being the scalar value, the rate of change, the second time derivative, etc.). At the next time step, a new state, with a "position" defined by a scalar, a time derivative, a second derivative, etc. each of which are uniquely defined from the previous state and the length of the time step.
For two different trajectories to intersect, the state at the point of intersection must define two alternative future states. But this is clearly impossible if the scalar and all of its time derivatives are identical. Thus, the best you can do is have two different trajectories approach arbitrarily closely. If I recall correctly, this argument was first proposed by Hirsh and Smale (1974).
One of the features looked for in a phase space portrait is groups of points on different trajectories which closely approach one another. In particular, we may find that there are regions of phase space towards which many different trajectories evolve, and these trajectories may each remain in one of these regions for some considerable time. Such regions may imply the existence of relatively stable (or metastable) states in the system, which is a possible predictor for future evolution of the system.
In order to determine whether such areas exist, we need to know if these neighbouring points on different trajectories are actually close to one another, or merely appear to do so because of the projection of our phase space.
Here we see hypothetical two-dimensional and three-dimensional portraits of the same system. In the two dimensional portrait, points A and B appear to be quite close.
In the three-dimensional phase space, we see that A and B are not close neighbours after all. If we made our interpretation on the basis of the two dimensional portrait, we would be in error.
In the diagram at left, points A and B are called false nearest neighbours. The presence of false nearest neighbours indicates that the state space is not defined in a sufficient number of dimensions (we would say that the embedding dimension is insufficient).
One therefore finds the embedding dimension by increasing the number of dimensions of our reconstructed phase space until there are no more false near neighbours.
The magnitude of the embedding dimension gives you an idea of the number of invariant parameters in the system--at least in an ideal world. Unfortunately, in the real world there is this thing called noise, which is infinitely dimensional; consequently ever higher-dimensional reconstructions reveal increasing numbers of spurious near neighbours which are demonstrated to be false in a higher dimension. One never reaches the point of having no false near neighbours.
So one may end up selecting an embedding dimension that seems reasonable. The estimate may be wrong, but can be assessed to a certain extent by studying closely the trajectories in higher dimensions using mathematical methods to laborious to discuss at this time.
I will discuss the use of probability density in phase space next time.
Hirsch, M. W. and S. Smale, 1974. Differential Equations, Dynamical Systems and Linear Algebra, Academic, San Diego, Calif., 1974.
This approach is choosing a suitable embedding dimension, which is the number of dimensions of state space into which we will unfold our time series.
Embedding dimension
The curves in the reconstructed phase space should not intersect, if they are unfolded in the correct number of dimensions. The reason for this will become plain if we once again consider the reconstruction in terms of a function and all of its various time derivatives. Suppose that a system is completely described in a state space. These dimensions will be the scalar measurement, its first, second, and higher time derivatives (speed, acceleration, jerk, jounce or snap, etc.--in the scalar sense).
Each state is defined by a "position" in phase space, with coordinates being the scalar value, the rate of change, the second time derivative, etc.). At the next time step, a new state, with a "position" defined by a scalar, a time derivative, a second derivative, etc. each of which are uniquely defined from the previous state and the length of the time step.
For two different trajectories to intersect, the state at the point of intersection must define two alternative future states. But this is clearly impossible if the scalar and all of its time derivatives are identical. Thus, the best you can do is have two different trajectories approach arbitrarily closely. If I recall correctly, this argument was first proposed by Hirsh and Smale (1974).
One of the features looked for in a phase space portrait is groups of points on different trajectories which closely approach one another. In particular, we may find that there are regions of phase space towards which many different trajectories evolve, and these trajectories may each remain in one of these regions for some considerable time. Such regions may imply the existence of relatively stable (or metastable) states in the system, which is a possible predictor for future evolution of the system.
In order to determine whether such areas exist, we need to know if these neighbouring points on different trajectories are actually close to one another, or merely appear to do so because of the projection of our phase space.
Here we see hypothetical two-dimensional and three-dimensional portraits of the same system. In the two dimensional portrait, points A and B appear to be quite close.
In the three-dimensional phase space, we see that A and B are not close neighbours after all. If we made our interpretation on the basis of the two dimensional portrait, we would be in error.
In the diagram at left, points A and B are called false nearest neighbours. The presence of false nearest neighbours indicates that the state space is not defined in a sufficient number of dimensions (we would say that the embedding dimension is insufficient).
One therefore finds the embedding dimension by increasing the number of dimensions of our reconstructed phase space until there are no more false near neighbours.
The magnitude of the embedding dimension gives you an idea of the number of invariant parameters in the system--at least in an ideal world. Unfortunately, in the real world there is this thing called noise, which is infinitely dimensional; consequently ever higher-dimensional reconstructions reveal increasing numbers of spurious near neighbours which are demonstrated to be false in a higher dimension. One never reaches the point of having no false near neighbours.
So one may end up selecting an embedding dimension that seems reasonable. The estimate may be wrong, but can be assessed to a certain extent by studying closely the trajectories in higher dimensions using mathematical methods to laborious to discuss at this time.
I will discuss the use of probability density in phase space next time.
Hirsch, M. W. and S. Smale, 1974. Differential Equations, Dynamical Systems and Linear Algebra, Academic, San Diego, Calif., 1974.

No comments:
Post a Comment