How life imitates the stock market, part 4; reconstructing phase space portraits

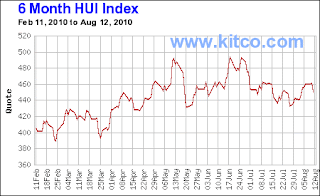
Here is the price chart for the last nine months for Detour Corp (DGC-T) [Disclosure: long]

Now suppose we decide we want to know something about what is driving the price of this stock. We have a time series (here we've plotted the daily closing prices for the last nine months or so). We think the dynamics of this time series might be interesting and are hopeful that if we were to learn something of them it might help us decide when or at what price we would wish to buy (or sell) this stock.

We know very little about what drives stock prices. If we were to guess at a conceptual model for the dynamics governing this particular stock price, it would probably include: the gold price; the perception of expected expenses in developing the property; the perception of political problems (native concerns or sudden mining tariffs, or somesuch); or the general perception of the overall stock market.

A sophisticated observer might want to add some stochastic element as well as something that takes into consideration the psychology of the observers interested in this particular stock. For we often observe that stock prices have a sort of momentum--when they have been stuck in a narrow range for some time, they are more likely to remain within that range, but if they break decisively, the stock price can be driven by "momentum", whether such momentum arises from investor herding or confirmation bias.

The tripping of a psychological switch allows for the prospect of some sort of feedback within our pricing system. All in all, it is beginning to look like the differential equations used to describe our system are going to end up being at least in part nonlinear. And the time series outputs from nonlinear systems are notoriously difficult to understand (or model).

So our system is affected by numeous factors, all of which we would like to at least have the potential to analyze. But all we have is price. Is it enough? Many commentators (this is not intended to endorse the services of the linked gentlemen) tell us all we have to do is watch price. But are they right?

It turns out that they are. I know, I can hardly believe it myself. I must admit I have some doubts about whether these commentators understand why price is all that matters, but also acknowledge that once you have an empirical  method that works for you, you may not feel you need to understand why it works. In fact developing such an understanding may only subtract from the amount of time you have to make money.

The reason why price is all you need is one of the deep mysteries of ergodic theory. In short, all information concerning the dynamics of all the inputs is recorded in all of the outputs of a system. Price is just such an output. Equally well, you might use volume or change in price, as these will both reflect the dynamics in which we are interested; however the relative weights of each component driving the changes in price may be different for each of these time series. But the information is all present in each series, so we should not gain very much by studying price in conjunction with one of these other variables.

Now the dynamics of numerous different factors are not revealed within a one-dimensional plot, which is all the above chart really is. We have stretched out time, but had we not done so, we would have ended up with something like this.

Not much to see here. All you could really make out is the highest price (the top of the line) and the lowest price (the bottom of the line)

In order to see all the dynamics of interest, we need to "unfold" the plot of the time series into a phase space plot with enough dimensions to reveal all the dynamics of all the factors influencing it. Normally you will need at least three dimensions to really see anything interesting. More practically, the plot should never intersect itself.

One way of unfolding the data is to plot it against some other data series which is related somehow, but which can be considered independent. By this I don't mean looking at parallel line charts--I mean a scatter plot of one variable against another.

For paleoclimate studies you might plot your proxy data for global ice volume against, say, your proxy for atmospheric CO2 and/or your proxy for deep ocean temperature (e.g., Saltzman and Verbitsky, 1995).

We don't have so many variables to choose from, so let's look at the closing price plotted against daily volume for DGC. One advantage we have over the paleoclimatologists is that by definition, both of these data series are sampled at the same intervals, and we can obtain both series over the complete interval of study (the last nine months here). You won't believe how much of a problem this can be in studying natural time series.

To create the graph at right, I have plotted the daily closing price against the daily volume for each day over the last nine months. The points are plotted in chronological order, and a curved line (as per tradition) is drawn through the points.

Each plotted point is called a state, and the graph itself is called a state space (alternatively phase space is also used). The curved line represents the trajectory of the system as it evolves through time.

What we have here is a state space of sequential price-volume states for Detour Gold Corp. from late November 2009 to late August 2010.

The beginning of the plot is somewhere in the tangle near $15. There is so much action there it is hard to see. The end of the plot is easier to see--it is the tail of the graph there at middling volume and a price over $30. Interesting, but hard to interpret.

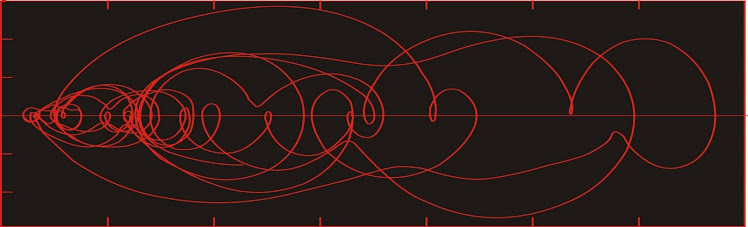
I could easily choose another data series to plot against price. This time I will plot daily price against the change in price from the previous close.

Here we actually have a plot that is easier to follow. Even though the beginning is hard to make out, there is little doubt about which way the system is evolving.

It is always moving clockwise around the loops, for the simple reason that below the horizontal axis, the price change was negative, meaning that the subsequent price is lower than the previous price.

Above the horizontal axis, the price change is positive, so the subsequent price must be higher than the previous price.

The further the curve is from the horizontal axis, the more rapid the price change. Consequently any area of stability must lie along or very close to the horizontal axis.

The above state space is very nearly a type that we would actually use. The only problem with it is that it is tilted slightly to the right, and this is because in calculating the price change, we use only a given point and the previous point. In principle, this price change should be considered valid for the middle of the trading day instead of the end. One way around this would be to calculate the price change over two consecutive trading days, and plot that against the closing price of the middle day. (So find the price change between Monday's and Wednesday's closing prices and plot that against Tuesday's closing price).

And let's divide the difference by two so we end up with an average price change over each two-day stretch.

This one is similar to the last, but a little simpler. That's because we have smoothed our first difference data somewhat.

But the overall features are the same. The system evolves as a series of clockwise overlapping loops.

Since we could have calculated the price change from the price time series, we could actually say that this is a state space which has been reconstructed entirely from the price data. This is the first trick discussed in the classic paper of Packard et al. (1980)--graphing a scatter plot of the original time series against its first (and higher) time derivatives.

Intersections are impossible in a properly reconstructed state space. The reason we have intersections in the state space reconstructions here is because we need to unfold the price function into at least three dimensions, and we have only done two (excel only allows scatter plots in two dimensions--so get to work Billy!).

This is the same method as I used to reconstruct the dust flux state space depicted on the masthead of this blog.

Were we to unfold the DGC price function into three dimensions using the method above, the third dimension would be the change of the price change (or the second time derivative of the price). If any further dimensions are required, we would use the third time derivative, then the fourth, and so on. Displaying data in more than three dimensions presents problems, but the data may still be studied using an entire toolbox of mathematical techniques which are well known (Abarbanel, 1997).

A plot of price change vs. price as we have done above is really a plot of x(n+1)-x(n) vs x(n). Could we not simplify the plot by dispensing the x(n) term on the ordinate? Can we not simply plot x(n+k) vs x(n), where k represents a lag? If we do, we end up with a plot (which is a reconstructed state space using the time-delay method) which looks a little different from the x(n+1)-x(n) vs x(n) graph (it is rotated 45 degrees, for instance), but the two plots are topologically equivalent.

In nature it is preferable for us to reconstruct the state space by the time-delay method because the errors in the second and higher dimensions will be smaller than if we reconstruct the state space using time derivatives. Arguably there is no error at all in the closing price, so it may be that there is no great advantage in using the time delay method for analyzing stock prices.

If we are going to use the time delay method, we have to decide on a value for k, which is called the lag. There are prescribed methods for doing so. Just as for a simple Cartesian graph, the x and y axes are perpendicular, so too for a good state space. The axes will be as close to orthogonal as possible if the average mutual information is a minimum. Hence the value of k chosen is the one for which the average mutual information between the time series and the lagged time series is a minimum.

Did you look at that equation? What many do instead is calculate the autocorrelation function of the time series for several lags, and choose a lag for which the absolute value of the correlation is a minimum. For many data sets, especially data sets which are almost periodic, the lag obtained in this manner will be very close to the optimum lag. Furthermore, the method is actually somewhat forgiving.

Does the time series of closing price show almost-periodic behaviour? Our graph for DGC does not appear to do so, but it is rather dominated by a long uptrend so it may be hard to say. There is reason to suppose that other stock prices may have such behaviour due to the relatively predictable recurrences of the weekend, month-end, seasonal, and year-end periods, and the periodicity may be a function of the timing of options settlement.

In the plots from the three earlier parts of this series, I have used a lag of four days. This choice was somewhat arbitrary. In the next part we will look at the DGC data with several different lags.

Universities: What's wrong with them?

An article here questions the wisdom of the University system in the modern world. It approaches the question from a historical and Catholic slant, given the importance of the University system of the Middle Ages, adding the question of what happened to them.

Today I would like to use some of my previous experiences in the university system as instructor, TA, grad student, (and undergrad) to discuss the reason that universities no longer perform as they used to. My experiences are coloured by my Canadian experience, and some of my observations may not necessarily apply to universities in the US or other countries.

I believe that the fundamental change in universities occurred when they became State-funded institutions.

When the university system began, its only objective was to train priests. Apparently, it did so very well. Over the last several hundred years, universities began to train other types of professionals, and currently some professions require a tremendous level of technical sophistication. Interestingly, despite the concentration and specialization that now occurs in technical training, university graduates are surprisingly useless in the business and technical world. How can this be?

I would submit that in the early days of training priests, the students were taught to read and write, and debate (or comment on) articles of history, philosophy. The trainees obtained a deep knowledge of their subject matter, and debates and commentaries made them proficient in writing, extemporized discussion, argument, and rhetoric.

One of the defining conditions of the early universities was their independence of local and papal authority. This concept is continued today in the institution of tenure, as well as the general belief that universities, despite being funded by the State, should not be controlled by it.

Tenure is a topic that has generated a great deal of debate. In principle, it is intended to broaden academic freedom by protecting professors from dismissal if they pursue unpopular forms of research. There are those who protest that it can lead to laziness on the part of professors who achieve it (a risk taken by the research institution); also those who protest that tenure has actually narrowed academic freedom, as young researchers must adhere closely to the norms of their field in order to survive their tenure hearings (Michaels, 2004).

(The same may be said about government grant applications).

New ideas emerged during the period from the Renaissance through the Enlightenment, one of the most important of which was the notion that the world could be investigated using the tools of observation and reason; furthermore, natural phenomena could be understood and explained purely in terms of material causes (i.e., no longer necessary to describe occurrences as "the work of God"). Simultaneously, the currently accepted "scientific method" came to be selected as the preeminent technique for understanding natural phenomena.

Where should these new practitioners of science work and teach? They naturally gravitated to the universities, as that was where most of them had been educated. Indeed, much of what we now call science was developed by individuals training for religious purposes, and there was an underlying philosophy suggesting that Honour was done to God by learning as much as possible about His Gift of the World.

Unfortunately, politics entered the academic world as soon as there were academic honours to be had. For instance, the Royal Society came down hard on Liebniz for daring to publish on calculus before the great Newton, which greatly influenced our thinking about the nature of the Universe (part of which I have discussed here).

The addition of a secular approach to science to the place of religious training did not significantly set back the university system. When I look at the problems that universities have today, they mostly come down to one thing.

Money.

Why didn't universities in the Middle Ages have the kind of cash flow problems that modern universities have? Firstly, they were financed differently. There was some money that may have come from the early State, but most money came from parishes (i.e., donations) or from fees and tithes paid by the students themselves. Nowadays, most universities receive operating funds from the State. Research money is also granted to individual faculty by the State, sometimes with unfortunate consequences.

Today, universities have three functions, each of which interferes with the others.

Firstly, they are there to provide instruction. Obviously. They are presented as such to taxpayers, who are responsible for the bulk of their funding. This funding will only be willingly provided so long as middle-class parents are convinced that their children will receive a good and useful education there. If fees rise too much, or if there is a sense that the universities are not there primarily for the education of students, there will be a backlash against them.

Secondly, they are to be centres of academic research. Here is the first problem: in my time as a grad student at the University of Toronto and at Memorial University of Newfoundland, it was abundantly clear that as far as the university and faculty were concerned, academic research was the sole purpose of the university. The teaching of students was something to be avoided (and which could definitely be avoided by the more important faculty). Unfortunately, the middle-class taxpayers who fund the university are under the delusion that the academic research at the university is a secondary priority which is only carried out insofar as it leads to improving the quality of education received by the students at the school.

(If not for the problem of  money, the combination of teaching and research at one place works. I found that teaching could be a galvanizing influence on research and vice versa.)

The third function of universities arose once they became funded by the State. Once this happened they became an agent of State power, and a reflection of prominence of the State. Initially this wasn't so bad, as they were well-funded. But once funded by the State, universities fell into a trap--they were no longer free to set tuition as high as they would like.

In the past a university might charge enough for tuition to be able to afford the best teachers and the best research facilities. For a short time after the conversion to a State-funded enterprise, they were sufficiently funded to continue. But over the years, the State funding as a proportion of the university's total budget has declined; there is increasing political pressure against raising tuition (with the "everyone should be able to get a university education" mantra); and poor economic performance has shrunk endowments and pension funds--all of which has put severe pressure on the budget of the modern university.

So the third function of the university is to be a machine for raising money. In fact, this is now the highest purpose of the university. Of course, the university wishes to project the image that teaching is its highest purpose. To increase the university's coffers, it is necessary to lower costs wherever possible. As the principal cost to the university is the salaries of its faculty, the best way to lower costs is to find ways to reduce the pay of the highest salaried faculty, which may be done by reducing their teaching loads and increasing the number of courses which have large numbers of students serviced by a minimum of teaching resources.

For instance, in my last years teaching, I found myself teaching courses of 500 or more students, armed only with two TAs who were given a total of about 100 paid hours for all marking and course administration. The lack of TA hours meant that there was very little marking per student, a factor which lead to all evaluation to be via multiple-choice exams.

Multiple choice exams are just dandy for "testing" on the cheap, but they aren't helpful in determining whether the student has any depth of knowledge of a subject. These students could not be receiving a great education. What's worse is that the number of this type of course has only grown, for the simple reason that they only cost about $15,000 in human resources (plus a fixed cost for class space) in exchange for which the university receives $500,000 in tuition fees.

There was one semester where I taught two such courses as well as three smaller courses ("real" courses, including lab work or essay writing).

Now to be fair, there are real courses in the university. One course I particularly enjoyed teaching was a senior-level course in the philosophy of science, which was aimed at students who were planning to move on into graduate school. My own education lacked such a course, and it was only near the end of graduate school that I began to appreciate how much I could have used it. This course used nearly the same level of human resources as the 500+ student course, but this one only had about fifteen students. (My other favourite course from this time was about logic and formal systems).

Clearly the large courses are being used to subsidize the teaching of the smaller ones. But that isn't the only form of subsidization.

In Ontario universities in the 1990's, the amount of government funding for a graduate student was approximately five times that of an undergraduate. At the time, tuition might have been about $4000 Canadian for a full year, but the government funding for an undergraduate was about $6000 per year, but the university received over $30,000 per year for each registered graduate student. The funding disparity led to what appeared to be a cynical ploy to "harvest" graduate students for their grants.

The information below came to me during contract negotiations for an Ontario TA union in the 1990's and may not exactly reflect what is happening at present in Ontario or anywhere else.

There were restrictions placed on graduate students--any grad students gainfully employed for more than ten hours per week would not be funded--consequently the university placed restrictions on grad student employment, the key one being that they could not be paid for more than ten hours per week. The universities have always maintained that this policy (see section 1.3) is in place in order to ensure that the student would progress satisfactorily.

Since employment income was the only income for many graduate students, as teaching assistants they had to paid a very high hourly wage in order to get by. Any student caught working more than ten hours per week could be removed as a full-time student. Depending on the department, loss of full-time status could mean loss of office space and other departmental support.

Furthermore, the funding for graduate students had a limited duration--two years for Master's candidates and four years for doctoral candidates (IIRC). In some departments at one of my former universities, it was common for students who overran these time limits to suddenly lose most of their privileges, the end result being that such students were far less likely to succeed in acquiring their degree. From the department's perspective, such students were no longer a resource and it was necessary to remove them so that fresh graduate students could be planted. (For the record, the geology departments at my previous universities did not engage in such behaviour, but there were numerous other departments which did, particularly in the Arts).

Such behaviour certainly gave the appearance that the university was interested merely in harvesting whatever funding the government granted for the students, but had little care whether there was a delivered product (in the form of a freshly minted M.Sc (or M.A.) or Ph.D.

Also, universities had an interest in increasing graduate student enrollment, possibly at the expense of undergraduate enrollment. As graduate students are involved in research, academic research becomes more important than undergraduate research. Again--the universities will tell you that this is not so, because the typical middle-classed parent is not as interested in graduate school for their kids as they are in undergraduate or professional school.

State funding and the poor economy (itself a reflection of State involvement) has made universities dependent on alternative methods of funding and has drawn so much of the university's efforts that its twin functions of teaching and research are significantly impaired.

References:

Michaels, P. J., 2004. Meltdown: the predictable distortion of global warming by scientists, politicians, and the media. The Cato Institute, Washington, D.C., 275 p.

How the game is played, part 3: Should you follow your brokers advice?

This is the third in a series of unfortunate events.

I had a friend who used to have a broker he called the Great White Shark. This broker was so unreliable that he was actually reliable, provided you always did the opposite of what he suggested. Whenever he advised you to sell a stock, it soon went up; whenever he advised you to buy a stock, it soon went down.

What was going on? Basically, the broker was working for his firm's interests as opposed to his clients'. When the firm needed to push some crap financing out the door, they advised their clients to pick up the shares, and if the firm knew something good was coming down the pipe, they took the shares off their clients' hands.

Last year, I received a communication from a broker about a small account which had not been active for some time. In it I held a few shares of a company called Volta Resources Inc. (VTR-T) which had been in the account for some years. The value of the shares at the time of the notice was not very much, as the shares were trading in the $0.15 range. [disclosure-- long position, but not as long as it could have been].

The communication stated that as I had not been active in this account for sometime, and as its total value was rather low, they gave me a choice of either selling the shares and closing the account or keeping the shares and the account open, but paying a monthly fee (I think it was about $20).

Neither choice seemed appealing, as the broker's commission was normally in the $60 range. But they said they would waive the commission in this one particular case if it would help me decide to sell my shares. What swell guys!

So I sold them at $0.19. About a week later the shares popped up and have continued popping up ever since (see below).

How the game is played, part 2; Why your broker can't get you in on that sweet private placement.

Today we look at yet another technique through which the sophisticated money picks the pockets of the unsophisticated. This one is a little worse than last time, because this time the sophisticated money is someone owing a fiduciary responsibility to the unsophisticated money.

The lesson today comes courtesy of the Toronto Stock Exchange. Go to the tsx website. Find the section that lists the largest short positions. I've placed the link here for you, but I find it by typing in "short positions" in to the search TMX.COM box. Now click on the report posted on March 18 ("Top 20 Largest Consolidated Short Position Report - March 15, 2010").

Yes, I could have sent you directly there, but I want you to have confidence that this data really exists and is not simply something I have made up.

The third entry on the list is Dundee Precious Metals (DPM). [Again, for disclosure, I have no position in DPM, either long or short]. We notice that the short position increased quite a bit during the reporting period, which is from February 28 to March 15. On February 28, the short position was 1,558,760 shares, and on March 15 the short position was 21,634,118 shares, for a net change of 20,075,358 shares.

Wow! A lot of people suddenly decided they didn't like this stock.

Still on the TMX website, get a quote on DPM. From the quote page, click on the price history tab, and then enter a date just after March 15, 2010 so you can see all trades over a 30-day period. We are interested in the trading that took place between February 28, 2010 and March 15, 2010. If you add up all the trades, you see that there were less than six million shares traded over that period.

Well WTF?! How do you increase the short position in a stock by 20 million when only 5 million trades take place?

Here's a game that some brokers play. Stock ABC announces good results, and a lot of buying comes in, so the price jumps. You call your broker, and tell him you want to buy 5,000 shares (let's say) of ABC. The broker says sure, gives you a quote, you send in the money.

Now your broker has been around a few years, and he has seen all this before. He knows that the price of ABC is going to fall soon, so he takes your money but doesn't exercise the trade. He scratches out an IOU for the back office so that any future statements in your account will reflect the presence of these shares. But no trade has occurred. Your broker believes that ABC will fall later, and he will buy the shares later at a lower price, put them into your account, and make some extra money for the brokerage. Is this acting in your best interest? Is this fulfilling his fiduciary duty to you?

In acting in this way, your broker creates a type of "synthetic short position". You are owed shares, yet no official share transaction has taken place. You would have no way of knowing that this is happening unless you call for delivery of your share certificates, because your brokerage statements will state that the shares are being held for you even though at this moment they are not.

This is fraud.

Virtually all the time, things work out for the brokers. ABC falls in price, the brokerage makes some extra money. Once in awhile the opposite may happen, and the broker is forced to buy at a higher price and takes a slight loss.

What happens if ABC now hits an enormous company-making hole and the stock rockets up by multiples? And what if the broker has not only done this in your account, but in a whole pile of client accounts, some of which may be owed a very large number of shares of ABC. It is possible that the brokerage may go bankrupt and you may not recover much of what you are owed. And the whole thing will probably be treated as an accident.

But it was fraud.

How might the brokerages protect themselves against a sudden rapid rise in the price of ABC?

Let's look at Dundee again. Go back to the quote, and this time click on the News tab. We are interested in news releases of the company this time. And we note that on February 22, 2010, DPM announced a bought-deal financing of 20 million units at $3.30. On that day, the share volume was rather high, and the price fell to basically the offering price.

Perhaps it is only one of those coincidences that the size of the offering happens to be the amount by which the short position grew by mysterious means over the three weeks until the offering closed on March 15. Or maybe it was one of those coincidences.

In this case it means that the brokerages sold the soon-to-be-issued shares to their clients. Which seems reasonable, as there were no warrants, and there are not reported to have been any brokers warrants offered to the brokerages, and the sales between February 22 (when the deal was announced) and March 15 (when the deal was closed) were all near the offering price; so the brokers did not overtly scam their clients.

The brokers did, however, put their clients at risk. The clients must have been sold undeliverable (by virtue of being nonexistent) shares. In a traditional offering, the clients' money would have been held in escrow until the offering closed--the money would be passed on to the company only when the shares were issued, and no short position would have been created. If for some reason the financing fell through, the money would be returned to the clients and they would lose nothing except an opportunity cost for the two weeks or thereabouts their money remained in the hands of the escrow agent.

But for things to work this way, the brokerages would need to find qualified investors willing to buy 20 million shares ("qualified" investors are sometimes called "sophisticated investors"--you are automatically considered sophisticated if you have more than a certain amount of liquid assets, or your annual salary exceeds an arbitrary amount--thus a wealthy orphan is a sophisticated investor, but you, who have been trading shares for twenty years, are not).

For the bought deal, the brokerages buy the shares, but in this case they pre-sell them to any and all of their clients, many of whom would not qualify as "sophisticated investors". Now what would happen if the deal is announced, the clients try to buy in but are filled with the nonexistent shares (creating the 20 million share synthetic short position) and then for some reason the deal doesn't happen? Suddenly all these clients are owed shares, and the scramble to cover could lead to an extreme market dislocation.

Once again--in this particular case, it would be unfair to call this a scam. But the electronic trail left suggests that the brokers did put some risk on their clients without any apparent compensation, which seems to be a breach of fiduciary duty. Furthermore, the clients who took on this risk were probably not "sophisticated investors", otherwise why not simply have them participate in a financing?

It is easy to see how the process can be used unfairly.

You call your broker because you've heard about this financing by ABC, in which units consisting of a share and half a warrant are being offered. You want in, but your broker tells you the offering is oversubscribed, too bad, but advises you it is so hot you should just buy shares, even though they are priced higher than the offering price. They could go higher still in the coming days because ABC is on a real tear, and with the financing complete they will advance . . .  blah, blah, blah.

You pay your money, your broker puts an IOU in your account and then later delivers shares from the financing to your account, skims a little extra profit, collects the warrants you should have had, and possibly some brokers warrants too. Not bad!

Thanks to Terry for doing the original legwork.

Next time we look at a simple game some brokers play.

How the game is played, part 1: Beware of stop losses

If money were stable and real interest rates were greater than zero, we would all keep our money in the bank. We might, once in awhile, invest a little money in the stock market, and the form of that investment would probably be a dividend-paying stock.

Unfortunately, none of the above are true, so we are forced to gamble with our life savings in the grand casino we call the stock market--our only alternative (unless you buy gold) is to watch the value of our money evaporate at the same rate irrespective of whether it sits in the bank or is stuffed under the mattress. And, like any other properly run casino, the game is rigged--or at least the rules are defined in such a way as to swing the odds heavily in favour of the House.

Today we will discuss one mechanism by which the House wins at the expense of its clients. In future entries we will look at least two others (more if I can find suitable examples).

Go to the TSX website. Get a quote on VTR (Volta Resources Inc.). In the interests of disclosure, I am long this stock, but otherwise have no involvement with them (but my long position is not as long as it should be for reasons that will be discussed in part 2).

Now click on the tab marked "Price History". You will see the price history of this stock for the last month. Scroll down below the table and you will see a little box labelled "History snapshot for Volta Resources Inc." Beneath it is a box. Enter the following date: 09/24/2009 and click the Get Quote button.

Here is what you should see:
Thursday, September 24, 2009
Closing Price:     0.405
Open:                0.450
High:                  0.460
Low:                  0.265
Volume:     3,142,884
Split Adjusted Price:     No splits
Adjustment Factor:     No splits

If you look at the previous two days you see that this stock underwent a tremendous move from $0.17 to about $0.45 in two days under heavy volume (about double the volume above). This was in response to an excellent news release.

Compared to the days before, and the days after, the trading on September 24, 2009 was really unusual. Both of the two previous days, the stock opened at or very close to the low of the day, rose through the day, and closed at or near the high. On the 25th, the stock traded within a small range as it fell from $0.42 to $0.39, trading only as low as $0.36.

But on the 24th, the stock opened at $0.45, rose to $0.46 until late morning when the price suddenly collapsed to $0.265. The collapse was on a relatively few trades with low volume, and there was a sudden cascade of 200,000 shares at $0.265 or $0.27, and then the stock rose rapidly on large volume back to $0.40.

Somebody was taught an expensive lesson.

What happened was this. Someone bought a lot of shares, probably at around $0.40 the day before, and they put a stop-loss on those shares, set at, say, $0.27. Now you and I cannot see that position, but there are people who can. There is usually a flurry of trading early in the morning, so the stalker waits until the activity grows quiet before making its move.

The stalker might place a bid just below the stop-loss (say $0.265). Then the stalker readies his computer, and fills all the existing bids down to the bid just below the stop-loss. That last transaction triggers the stop-loss, and the stalker is right on it picking up the stop-loss shares. Because VTR was thinly traded, the entire affair was stretched out over a couple of hours, but I can remember on several occasions in 2003 seeing the same thing happen with Couer d'Alene (CDE-N), and it was clear that all the bids were hit and the stop-loss triggered in less than a minute (Disclosure--no current position in CDE-N, long or short, although I was long in 2003). It would then take about fifteen minutes for the stock to return to (or near) the price before the quick takedown.

This is an example of how sophisticated money takes advantage of unsophisticated money.

In the medium to long term, seeing this type of activity is a bullish sign for the stock in question, as it means that sophisticated investors are picking the pockets of the unsophisticated in order to accumulate the stock cheaply. It is, however, a mark of the unfairness of the market (or at least the imbalance of information available to certain players at the expense of you and me).

There are a couple of lessons we can learn from this:

1) don't actually post your stop-losses. Keep them in your mind only (actually this isn't likely to be a problem until you are wealthy enough to buy positions large enough for this sort of character to take an interest) as Jim Sinclair has suggested;

2) It can be very useful to keep stink bids in 15-20% below the going price of a stock, especially a strong one. Your bid will get filled in the course of the takedown. Part of my current long position in VTR was obtained during a similar takedown (albeit at a higher price).

Emergence in Biologic Systems--an Example

Every so often here at the World Complex, we like to take some time off working on the relatively simple problems of climate change, earthquake prediction, the dynamics of interrelated economic systems, and sudden state changes in everything from wind patterns to empires; and focus on the really challenging problems of life.

Such as--how does this happen?

Amelia, aged 11 months.

Amelia, aged 10 years.

And how does it happen so fast?

How life imitates the stock market, part 3

This is the third part of a series about applying analytical methods developed for dynamic systems (like climate) to the stock market.

In our last installment, we were looking at the recent price history of the stock of a company called Nautilus Minerals Inc. and I presented a phase space portrait in two dimensions of the price action over the last four months (note that phase space and state space are often used interchangeably).

2-dimensional phase space portrait of the share price of Nautilus Minerals Inc. from April to August 2010. Look at those rabbit ears! That's what you get from a singular spike in the data. It would be worse in three dimensions. There would be a third spike coming right out of the screen.

The plot above begins in April (the curve starts at the little tail sticking out beside the "April" label above. It actually remains in the grey area (a Lyapunov-stable area, or LSA) near the middle of the plot through most of April making small straight side-to-side and up-and-down motions with a magnitude of about 10 p.

At the end of April, the price state drops out of the upper LSA and meanders its way through phase space towards the lower LSA, in the 100 p range, which is reached in late-May. The price state remains within this lower LSA until about mid-June, then abruptly rises, and by the beginning of July, it appears to be headed back to the upper LSA.

Then comes the sudden price spike. The price state veers up, down, then sharply right, and back left, veers around the upper LSA before plunging into it at the end of July and it has remained until the end of the analysis, which ended early in August.

The price spike seems to have simply resulted in a short-term (one month) detour around the higher price state areas of phase space, but probably did not have any effect on the ultimate destination. Of course, for those who were unfortunate enough to buy at the top of the spike, well . . . sorry about that.

It is extremely rare to see the rabbit-ear formation in these charts, in natural functions. I have seen it only once in some marine core data. Spikes like that are rare in nature, which is hard--so far as we know  ;) -- to manipulate.

What actually is interesting is the drop from the upper LSA to the lower LSA and the subsequent return. What happened in that interval? Was there really a change in the perceived value of the company between April and June (and then again between June and August)? Was this a seasonal junior gold fluctuation?

Let's compare NUS against HUI. It isn't entirely a fair comparison, as NUS is not in commercial production. But we may be able to use HUI to get an idea of the mentality of the gold stock market. It might be better to use gold, or possibly BMO's new junior ETF, but I have numbers for HUI.

HUI chart for six months prior to the writing of this blog entry. There's no link through because I don't want the chart to update. An updated chart is available here.





The reconstructed phase space portrait for the HUI index is presented below. The graph isn't perfect, because I digitized the plot from the above graph, but I believe it will prove to be a reasonable construct.

The HUI reconstructed phase portrait from February until early August looks a little complicated. I have coloured different segments of the curve in different colours so it is a little easier to interpret.

There are two obvious areas of concentration--the area in phase space bounded by about 440 and 460 on both axes, and the area bounded by about 400 and 420 on both axes. Both of these might be considered to be LSAs. There may be a third above 480 on both axes but would need to see more time spent there first.

The system occupies the lower-priced LSA in the early part of the graph, and moves up to the higher-priced LSA at the end of April and remains there except for a few excursions to still higher prices in mid-May and late June.

So where Nautilus showed a steady decline through May, HUI was confined to the higher-priced LSA. When NUS began to rise in late June, this was in tandem with a similar rise in HUI. The spike in NUS was unique to itself.

The behaviour of NUS in May and June may be related to company news. In May, NUS announced that it had demobilized one drilling vessel and was seeking bids on another. Shareholders may have interpreted that this would be some time before there were to be any new results, leading to a drop in share price. The announcement in mid June that a drilling contract was signed suggested that activity would be renewed, which led to the rise in price towards the higher LSA.

One other note about phase space portraits, which I have not previously emphasized. There is no mathematical magic. The phase space is just a different presentation of the data. What appears as a cluster of scribbles in a LSA appears as a discontinuous series of price fluctuations in the original data series--what analysts might call a resistance level (which later becomes support after the price rises through it). Compare the higher-priced LSA in the HUI phase space to the original HUI plot. There are a lot fluctuations between 440 and 460, and these are manifested as that tangle of curves in the area between 440 and 460 in phase space. Later on we will see how the dynamics of a complex system manifests itself in similar areas of "resistance" and "support" even in natural time series.

Blowing Up the Arctic

Today marks the 25th anniversary of the end of my first real geological project, in which I got to detonate explosives in a pristine landscape--in Canada's High Arctic. And since another ice island is in the news, what better time than to take a trip down memory lane?

Map of part of the Canadian High Arctic. Plundered from here.












I spent several months living in a camp on an ice island--a chunk of ice that calved off the Ward Hunt Ice Shelf on Ellesmere Island (northernmost island on the map) drifted southwest and at the time I was on it, was roughly between Ellesmere Island and Axel Heiberg Island, and over the summer months moved southwest off the coast of Axel Heiberg Island. The hope was that the block of ice would circumnavigate the Arctic Ocean and we would get a "free" ride enabling us to survey and sample the seafloor there.

It didn't quite work out that way.

Instead the island (which was about 5 km long and over 40 m thick) drifted into the sound between Meighen Island and Axel Heiberg I., eventually grounding and breaking up.

A photo of the ice island in 1985, taken from a book about the Polar Continental Shelf Project, which administered it. The ice island is the relatively smooth area with the long "ripples". 




Although I flew a number of times to and from the thing, I never got a very good photo (those were the days when digital photography was just a dream).

The actual ice island in the photo above is surrounded by multi-year ice (the rougher looking stuff). The ice island itself is relatively smooth.

Landing a plane is no problem, once you've smoothed off the surface. Driving around on it on snowmobiles, hauling equipment equally so. Here we are, drilling and casing shotholes in the ice.

The multi-year ice is thinner and rougher. There is a definite (but smooth) drop as you run off the edge of the island onto the multi-year ice. The landscape is a lot more rugged as well.

The area is pretty bleak. Other than people I think I saw two arctic terns all summer. And once there was a long trail of footprints of some small animal checking out some of the cable we left lying around.

What were we up there for?

There was an idea that having a research crew on a piece of arctic ice would be a really fine idea. For our project, the idea was to carry out a seismic survey to understand the crustal structure beneath the Arctic Ocean, taking advantage of this large block of ice that was going to circumnavigate it. We wouldn't have any navigational control, but the thinking was that we would nevertheless get some valuable data.

And if it happened to enhance Canadian sovereignty, so much the better. It was, after all, the year of the Polar Sea incident.

From the article referenced above:

"The most direct challenge to Canada's sovereignty in Arctic waters came in 1985, when the U.S. sent its icebreaker Polar Sea through the Northwest Passage without informing Canada or asking permission. The political skirmish that followed led to the 1988 Arctic Co-operation Agreement between the two countries. Boiled down to its essence, the agreement said the U.S. would not send any more icebreakers through the passage without Canada's consent, and Canada would always give that consent. The wider issue of whether Canada's Arctic waters were internal or international was left unresolved."

Read more: http://www.cbc.ca/canada/story/2009/02/27/f-arctic-sovereignty.html#ixzz0wK7O4zhs

For us this meant that there were some job openings for recent graduates. Six of us were selected, three from UWO and three from U of S. We were asked to get firearms acquisition certificates (easy then, very difficult now) and blasting permits, although due to time constraints they dropped the latter--we were given some half-hour of on-the-job training in explosives handling and off we went.

Those really were the days!

The first thing we did when we were there was have a shooting contest. I won, was declared camp marksman, which didn't turn out to be nearly as much fun as I would have liked. Mostly it meant I was tasked with periodic oiling of all firearms on the island, in addition to my other duties, which were mostly preparing to blow up the Arctic and then actually blowing it up. In theory, I was also tasked with shooting anything that might show up and pose a danger to us, but the only other animals were the two aforementioned arctic terns, which would have been difficult to represent as dangerous, and they didn't stick around long enough for me to arm myself in any case.

Flying to the ice island from Resolute (home base of PCSP) via Twin Otter. Note skis.

The experiment required us to set up explosive charges in sequence underwater. The shockwaves would bounce around in the water column, but at least some of the energy would penetrate the seafloor and be reflected from rock layers within the Earth, allowing us to infer subsea structure. So we would need to install the means to set off the explosives and the instruments to detect the sonic returns (sensors called geophones).

The first part of our work was installing the sensors, which involved a great deal of digging. There were to be at least 120 stations, each of which required nine geophones, eight in a circle (as at left) and one in the middle. 

The stations were each about 30 m apart and had been surveyed and marked before our arrival. You might see the stake near the centre of the photo.

The lasting legacy of this job (for me personally) is that I was able to impress my future wife with my digging prowess when she installed a garden some fifteen years ago. I was like the Shoveler.

The holes were dug through the snow cover down to the ice surface. In most places this was no more than a couple of feet down, but at one end of the array we ran into an old drainage channel, and there had to dig holes more than eight feet deep.

Once on the ice, the auger came into play, as we had to auger a hole down some six to eight feet or so, suspend the geophone in the hole, then fill it with water so it would freeze into place. The cables were suspended above the snow so we could hook them up later.

The cables were about 3 km long, so untangling them as they came out of the box was, shall we say, a chore. At 30 m intervals, there were nine takeouts, and these would be connected to the geophones that we had already buried. The other end led into the bank of computers in a special hut a couple of pictures up.

Next came the shotholes. We used a heat exchanger to melt a narrow tunnel from the top of the ice to the bottom, dropping out into the ocean. Now, since the ice island is about -40C in the middle, how do we keep the holes from refreezing?

The holes were lined with plastic tubing--about six inch diameter IIRC. The sections were screwed together until we had a continuous lined tube right through from the surface to the sea.


Then we filled the tubing with the Government of Canada's own secret blend of diesel fuel and trichloroethane (TCE). The stuff was a horror show. It soaked through your clothes, and was almost instantly absorbed through the skin and for a week everybody had a TCE hangover.


The mix was designed to be the same density as ice, so that as we filled the pipe, when the level of fluid within the pipe had risen to the level of the ice, all the seawater would have been displaced from the pipe. This blend had a freezing point well below the temperature of the ice, so the holes would stay open. 


Next the detonating cables were laid in. One end went to the data collection hut, and the other end of each went to one of the twelve shotholes. There was a lot of loose cable at the end, because the ends of it would be connected to the detonators, which were electrical. They would be fired from the hut. There was a circuit at the top of each shothole which allowed you to short the system so that you didn't accidentally fire off the detonator before the explosive was lowered down the hole.


Additionally, the detonators were of a special type that needed a fairly substantial voltage to fire, because static charges on snow could be large enough to accidentally fire off the standard issue detonators.


We were all a little tentative handling the explosive when we started off, but after a few days without anybody blowing up we really began throwing the stuff around. One of the guys even managed to crash a skidoo into a wall of dynamite boxes without mishap. Well, the engine cowling of the skidoo was crushed. I swear it wasn't me. But I did manage to sink a skidoo into one of the meltwater ponds.

Detonation control. Plug in the cable, charge the capacitator from the battery, select the station, and kaboom.

Things went swimmingly. As the summer progressed, the snow melted and the camp was surrounded by a lake of meltwater which we had to drain by drilling holes in the middle of camp. The original runway disappeared, and we spent some days making a new one. There were amusing and occasionally difficult issues with sewage and sanitation.

Meltwater was an ongoing problem as the temperature rose. Eventually we had to drain the camp.


The island shook itself free of the surrounding pack ice and began drifting. Every kilometre or so we travelled, we were to set off a series of explosions (ideally all twelve in sequence--though I don't remember how much time between shots).

There were several hitches that plagued the program. One of the most important ones was the reaction between the explosives and the TCE/diesel fuel blend. Since you had to punch a hole in the stick of explosive and insert the detonator, as the explosive was lowered through the special blend, there was an opportunity for some sort of chemical reaction to occur (which I infer from all the hissing and spluttering of the explosive when unexploded sticks were retrieved), and as a result occasionally when the detonator exploded, the explosive did not follow suit.

The work was hard on the cables, especially the ones that were constantly being connected to detonator cables. They would fray, or break, and I would have to strip insulation and occasionally solder the ends of the cables together. It was so cold that the solder would melt, or the flux, but never both at the same time.

Lastly, as the island was moving around, it was sometimes difficult for supply aircraft to find.

I had a two-week break in early June and when we flew back from Resolute (now Qausuittuq) we couldn't find the place. Fog had completely socked in the island during the flight. We flew in circles for awhile looking for it, but didn't have enough fuel to return to Resolute so we were forced to land at Eureka, which in comparison to the ice island, was paradise.

Eureka - paradise on Earth. Really. In mid-June, you have 24 hour sunlight, the weather is good, temperature mid-20s (C).





By July we were locked in fog and rain. The bright sun we had in the early days was due to the dryness and the cold (-30). It was warmer in the summer, but unpleasant. It was actually better when it was colder. You could even sunbathe--on top of the seismics hut where you were out of the wind in full sun you felt warm in a matter of minutes.

Ultimately papers were published. I remember looking a little bit at the raw data. One of the other students did an MSc thesis on the data. I later did my Master's in marine geology at MUN.

How Life Imitates the Stock Market, part 2

I am modifying much of this discussion from a paper which is currently under consideration for publication.

In the last installment we saw that certain complex systems are characterized by multiple modes of operation. Assuming that our system can be defined as a continuous system of differential equations, then it will evolve deterministically from each uniquely defined initial point to a unique sequence of successor states, implying that two states which lie on different trajectories will remain so—hence, no line crossings occur [Hirsh and Smale, 1974].

Any two different trajectories may evolve toward successor states which are arbitrarily close to one another. Thus they may converge toward a single state which does not change in time. This unchanging state is called an attractor, and the behavior is described as asymptotic stability, as the system tends to evolve asymptotically towards some immovable point. Alternatively, they may not converge onto a particular point, but the successor states from any state within a small region of phase space may stay within a small (but possibly larger) region of phase space. Such behavior is described as Lyapunov stability.

The conditions by which asymptotic stability occurs are extremely specific, and it is difficult on the basis of field observations of the climate system or of the stock market to be certain that our observed system demonstrates such behaviour.

A qualitative approach to interpreting dynamic systems includes describing the phase space in terms of the type, order, and number of attractors (or areas of stability) that are traced out as the system evolves through time. The ice volume phase space portrait of last time is an example of a system with a number of disjoint Lyapunov-stable areas (LSA), each separated in phase space by a separatrix. At any given time, the state of the system occupies only one such LSA, so that their number therefore constitutes the total number of alternative long-term behaviors, or equilibrium states, of the system.

Since an LSA is likely to be smaller than the total allowable range of states, the system tends to become boxed into an LSA unless it is subjected to external forcing. When the state approaches a separatrix, small perturbations can trigger a change to a nearby state, which can result in chaotic changes in the evolution of the system [Parker and Chua, 1989]. Thus very complex behavior can arise in multistable systems.

Probability density plot of reconstructed phase space portrait of the ice volume system compiled from the past 750 thousand years (filled solids) superimposed on the phase space plot of the last 120 thousand years (dashed curve). Regions of high probability (darker) represent LSAs and result from multiple visits to the same region of phase space, or by a drop the rate of evolution of the system. From Gipp (2001).

The typical approach is to label the LSAs and characterize the system as a series of steps from one LSA to another. If the LSAs in the figure are labelled (from lower left to upper right) A2, A3, A4, and A5, then the curve above might be characterized as evolving from A2 to A4 to A5, and is currently heading in the general direction of A2 once again.

The evolution from one LSA to another would not occur except in the presence of external forcing, which successively drives the system across a separatrix after which it evolves quickly towards some other LSA. Now let us consider application of this approach to the stock market.

Over long periods of time, a stock will typically trade within a range. Provided there is to be no change in the fortunes of the company, we would normally expect that small perturbations in the price will be countered. In this way, the stock price exhibits Lyapunov or even asymptotic stability. The market has a "perception" of the value of the stock, and any deviation from that value is arbitraged away. Arbitrageurs will therefore act as the negative feedback cycles that we infer for a complex system.

Reconstructed phase space portrait (price vs. lagged price) showing the trajectory traced out by one stock near a Lyapunov-stable area (LSA). Small arrows show the evolution of the system through time.











Nevertheless, the external forcing (information in the form of money) may be sufficient to perturb the stock price over a separatrix at which point it suddenly accelerates toward some new area of phase space. We would probably say that the stock has become a "momentum play", dominated by the momentum players who continue to push the stock rapidly in whatever direction it happens to be moving.

Price chart for the stock in the above phase space. The momentum players have carried it out of a trading range. How high can it go?





All momentum plays eventually come to an end, and if there have actually been no changes in the fortunes of the company, the reasonable expectation is for the price of the stock to return to its previous trading range. But there is no guarantee that it will do so by the most direct path.

Possible scenarios by which stock price may return back to a trading range after breaking out and momentum later fails. In scenario 1 the stock falls back to the LSA. In scenario 2 the stock goes on an excursion through phase space before returning to the trading range. In this example we are assuming that there has been no change in the perceived value of the stock.

We see two possible scenarios after the breakout. Infinite variety is possible, especially in terms of the excursion through phase space. For an example of a wild one, let's look at one stock. Should I name it? In the interests of full disclosure, the stock in question is Nautilus Minerals Inc. (NUS-V), which was possibly the object of a recent price manipulation. (Kudos also to IKN for this story). I have no position in Nautilus, but am on management of a company that might be perceived as a competitor (but isn't really).

Nautilus Minerals Inc. share price for the past four months in pence (sorry about that!)

We see a general downward trend until that rather singular spike corresponding to the punch line of an interesting promotion. Let's look at the two dimensional reconstructed phase space portrait.

Two dimensional phase space portrait of the NUS-V stock price since April. Lag is four trading days. There is a lot of dynamical information going on here, which I will go through in part 3 of this post, but note the two highlighted areas which may represent areas of Lyapunov stability, and that prior to the unusual spike of early July, the price trajectory appeared to be returning to the LSA that the price state held in April. DYODD.




References

Gipp, M. R., 2001. Interpretation of climate dynamics from phase space portraits: Is the climate system strange or just different? Paleoceanography, 16: 335-351.

Hirsh, M. W. and S. Smale, 1974. Differential Equations, Dynamical Systems and Linear Algebra, Academic, San Diego, Calif., 1974.

Parker, T. S., and L. O. Chua, 1989.  Practical Numerical Algorithms for Chaotic Systems, Springer-Verlag, New York.

Volcker-Bernanke puzzle no puzzle

In a recent article in the Asian Times, Hossein Askari and Noureddine Krichene, who I can only assume pass for economists, talk about the effects of interest rates on unemployment. They propose the existence of the "Volcker-Bernanke puzzle", which I will leave to them to describe. . .


"Assuming Fed chairman Ben Bernanke succeeds in reverting the US economy to full employment and rapid growth, then economic historians will be facing a difficult puzzle that could be coined the Volcker-Bernanke puzzle. Paul Volcker, Fed chairman from August 1979 to August 1987, got the US economy out of 11-12% unemployment by pushing money market rates to 19%. Bernanke pushed unemployment from 4% to 10% through aggressive monetary policy with near-zero interest rates, massive monetary injection, and buying all toxic bank loans; however, Bernanke, if he does succeed by his indicated path, will have pulled the US out of 10% unemployment by even more monetary stimulation."

Well, that certainly is a conundrum! But wait a minute. . . isn't that first assumption a little presumptuous?


"Somehow, either extreme, very tight or very loose monetary, could be followed by policymakers to solve the unemployment problem and propel the economy back to prosperity. It makes no difference which extreme is adopted!"


Amazing! No matter what we do, the economy will recover! Of course that doesn't explain how we got into trouble in the first place.


Maybe our problem was that after the fall of Volcker and before the rise of Bernanke, our interest rates were too moderate. They should have been either much higher or much lower! Now who was the guy in charge of setting interest rates back then?

I'm still not getting the puzzle though. On one hand, raising interest rates ultimately resulted in lower unemployment. On the other, lowering interest rates "pushed unemployment from 4% to 10%".

I still don't see a problem. One method produces lower unemployment, and the other produces high unemployment. Logically, you simply choose the method which produces the desired outcome. Given all the Ph.D. economists working on this, we can only assume that that indeed is what is happening.

So what is the puzzle? Our favourite economists again . . .

"Assuming Fed chairman Ben Bernanke succeeds in reverting the US economy to full employment and rapid growth, then economic historians will be facing a difficult puzzle that could be coined the Volcker-Bernanke puzzle."

Well always assuming that of course. We might also add  . . .

Assuming leprechauns exist, Obama's new economic plan wherein Federal agents are to be tasked with chasing rainbows in order to seize pots of gold at their ends will balance the Budget by 2012 at the latest.

It's hard to know on what basis this assumption is being made (the Askari-Krichene assumption, that is*). I hereby formally name this assumption after them with the sincere hope that it leads to their lasting fame.

Formally the Askari-Krichene assumption goes as follows:

"Assuming Fed chairman Ben Bernanke succeeds in reverting the US economy to full employment and rapid growth (which is precisely the opposite of what we are empirically observing), then economic historians will be facing a difficult puzzle that could be coined the Volcker-Bernanke puzzle."

We could add to their fame by creating an entire genre of logical statements that could be referred to as Askari-Krichene logical positions as follows . . .


If A is observed, then assume not A.

Which can be reduced to the Askari-Krichne Rule of Inference for Keynesian Economics:

If A then not A.



*The assumption about leprechauns follows from careful empirical observations.